你知道吗?最近在区块链的世界里,以太坊可是掀起了一股热潮。这不,算力大战又开始了,各种公式、算法轮番登场,让人眼花缭乱。今天,就让我带你一探究竟,看看以太坊算力背后的那些事儿。
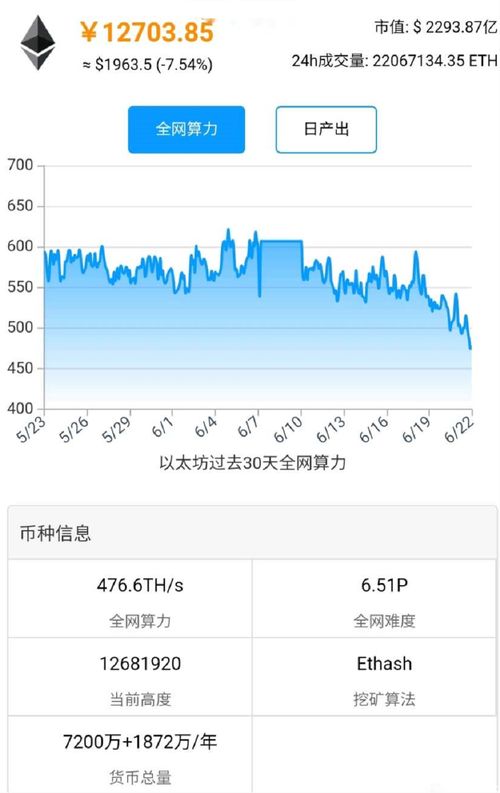
首先,咱们得弄明白什么是算力。简单来说,算力就是指计算机处理信息的能力。在区块链领域,算力更是至关重要。以太坊作为全球第二大加密货币,其算力自然不容小觑。
以太坊的算力主要来自于矿工。他们通过运行特定的软件,参与以太坊网络的共识过程,从而获得以太币奖励。这个过程,我们称之为挖矿。而算力的大小,直接决定了矿工挖矿的效率。
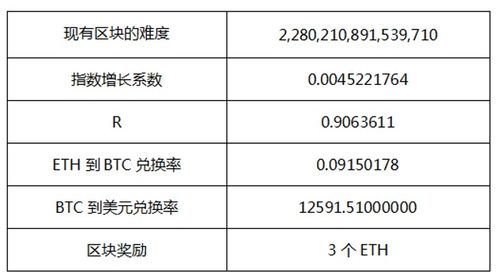
那么,如何衡量一个矿工的算力呢?这就需要用到算力公式了。以太坊的算力公式如下:
算力 = 挖矿速度 × 2^32
这个公式中,挖矿速度是指矿工在单位时间内成功挖出区块的次数。而2^32是一个固定的系数,用于将挖矿速度转换为算力值。
举个例子,如果一个矿工的挖矿速度是1次/秒,那么他的算力就是:
算力 = 1 × 2^32 = 4,294,967,296
也就是说,这个矿工的算力达到了4.29亿。
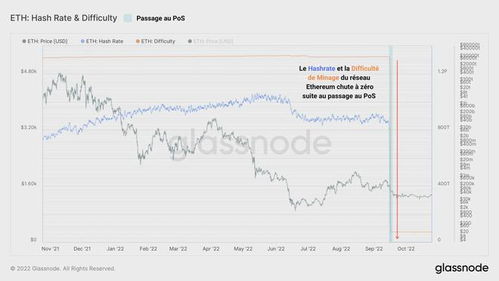
随着以太坊价格的上涨,越来越多的矿工加入了这场算力大战。他们纷纷购买高性能的挖矿设备,以提高自己的算力。
算力大战并非一帆风顺。一方面,矿工们需要承担高昂的电费和设备折旧成本;另一方面,以太坊网络的难度也在不断调整,使得挖矿难度越来越大。
为了在算力大战中脱颖而出,矿工们使出了浑身解数。有的矿工选择购买大型矿场,集中资源提高算力;有的矿工则通过优化算法,提高挖矿效率。
那么,以太坊的算力公式究竟有何秘密呢?其实,这个公式的设计初衷就是为了保护以太坊网络的安全。
首先,算力公式中的2^32系数,使得算力值与挖矿速度成正比。这意味着,矿工的算力越高,挖矿速度就越快,从而提高了以太坊网络的共识效率。
其次,算力公式中的2^32系数,也使得算力值具有可扩展性。随着以太坊网络的不断发展,矿工的算力也会不断提高,而算力公式仍然能够适应这种变化。
算力公式中的2^32系数,还具有一定的抗攻击能力。因为,攻击者要想篡改以太坊网络,就必须拥有超过网络总算力的51%以上。而2^32系数的存在,使得这个目标变得遥不可及。
以太坊的算力是保障其网络安全的重要基石。而算力公式,则是这个基石的基石。在这个充满挑战的算力大战中,矿工们将继续努力,为以太坊的繁荣发展贡献力量。
那么,你准备好加入这场算力大战了吗?快来和我一起,探索以太坊算力的奥秘吧!