你知道吗?在数字世界的深处,有一种神奇的数学工具,它不仅让以太坊这样的区块链平台安全可靠,还能让我们的数字资产像魔法一样流转。这就是椭圆曲线密码学(ECC),一个在以太坊中扮演着关键角色的数学小精灵。今天,就让我带你一起探索这个神秘的世界,看看它是如何让以太坊变得如此强大的。
想象你有一个珍贵的宝盒,里面装着你所有的数字资产。为了防止别人打开这个宝盒,你需要一把锁。在现实世界中,你可能需要一个复杂的机械锁,但在数字世界,我们需要的锁要更高级,更安全。这就是ECC的用武之地。
ECC是一种基于椭圆曲线数学结构的加密算法。它利用了椭圆曲线的复杂性和数学特性,为我们提供了一个强大的数字锁。相比于其他加密算法,ECC在提供相同安全性的情况下,需要的密钥长度更短,这意味着它更快、更高效。
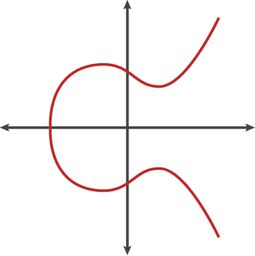
那么,什么是椭圆曲线呢?简单来说,椭圆曲线是一类满足特定方程的曲线,通常形式如下:
y2 = x3 + ax + b
其中 (a) 和 (b) 是常数。你可能觉得这只是一个数学公式,但它在数字世界中却有着神奇的力量。
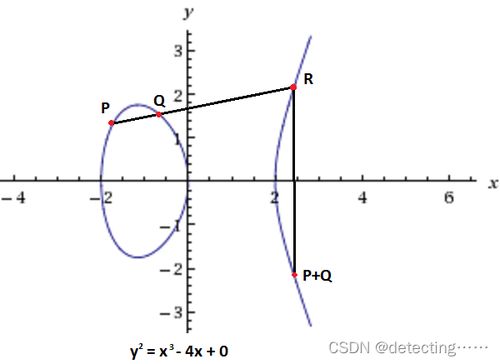
椭圆曲线上的点构成了一个阿贝尔群,这意味着你可以对这些点进行加法运算。这种加法运算有着独特的性质,比如结合律、交换律等。这些性质使得椭圆曲线在密码学中具有独特的优势。
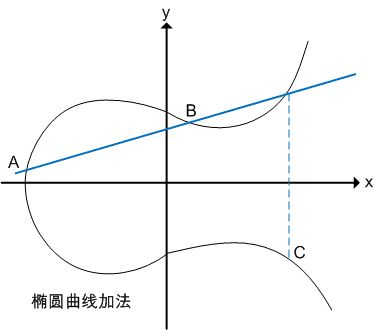
ECC的安全性基于椭圆曲线离散对数问题(ECDLP)。简单来说,ECDLP就是找到一个整数 k,使得 kP = Q,其中 P 和 Q 是椭圆曲线上的两个点。这个过程在数学上非常复杂,即使知道 P 和 Q,也很难找到 k。
这种数学难题正是ECC安全性的基础。因为如果有人能够破解ECDLP,那么他们就可以破解ECC,进而破解以太坊和其他使用ECC的区块链平台。
以太坊作为全球最大的智能合约平台,自然离不开ECC的支持。在以太坊中,ECC被用于多种场景,比如:
地址生成:以太坊地址是基于公钥生成的,而公钥又是通过私钥和椭圆曲线计算出来的。
交易签名:在以太坊中,用户需要使用私钥对交易进行签名,以确保交易的安全性。
智能合约:智能合约中的许多安全机制都依赖于ECC。
正是因为ECC的高效性和安全性,以太坊才能在数字世界中屹立不倒。
在以太坊中,ECC的一个常用应用是ECDSA(椭圆曲线数字签名算法)。ECDSA是一种基于椭圆曲线的数字签名算法,它利用ECC的特性来生成和验证数字签名。
ECDSA的核心概念包括:
签名:签名者使用私钥对消息哈希进行签名,生成两个值:r 和 s。
验证:验证者使用签名和公钥来检查消息的真实性。
ECDSA的工作流程包括链下签名和链上验证两个步骤。链下签名过程包括以下步骤:
1. 准备消息:计算消息的哈希。
2. 签名生成:使用私钥对消息哈希进行签名,得到 r 和 s(恢复参数)。
3. 传递签名:将消息和签名传递给链上或其他验证方。
链上验证的过程是通过公钥地址验证签名和消息的一致性:
1. 使用签名和消息恢复出签名者的地址。
2. 检查恢复出的地址是否与预期一致。
ECC和ECDSA是数字世界中的神奇工具,它们为以太坊和其他区块链平台提供了强大的安全保障。在这个充满机遇和挑战的数字时代,ECC和ECDSA将继续发挥重要作用,为我们的数字生活保驾护航。让我们一起期待这个数学小精灵带来的更多惊喜吧!